We assume that the glottal end is closed, but the mouth is open. This is the configuration we are referring to:
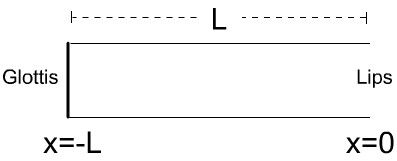
The acoustic tube is uniform, and its length is L. The glottis, located at x=-L, is closed (infinite impedance) and the mouth, located at x=0, is open (impedance zero). Now, pressure variation p(x) along this uniform acoustic tube is expressed as:
$latex \frac{d^2p}{dx^2} + \left(\frac{2\pi f}{c}\right)^2p = 0 ~~(I)$
where f represents frequency in Hz, and c is the speed of sound: $latex 3.53 \times 10^4 cm/s$ at 37° C.
According to the boundary conditions (the impedances at both ends), the solution is:
$latex p(x) = P_m \sin{\frac{2\pi f}{c}x} ~~(II)$
where $latex P_m$ is the peak in sound pressure. On the other hand, we have a relation between pressure and volume velocity
$latex \frac{dp}{dx} = -\frac{j2\pi f \rho}{A}U ~~(III)$
$latex A$ is a constant representing the tube’s area. Now, volume velocity can be expressed as
$latex U(x) = jP_m \frac{A}{\rho c} \cos{\frac{2\pi f}{c}x} ~~(IV)$
where $latex \rho$ equals the average atmospheric density ($latex 1.14 \times 10^{-3} gm / cm ^ 3$ at 37°C).
As U(−L) = 0, resonances Fn of the acoustic tube are
$latex Fn = \frac{2n – 1}{4}\frac{c}{L} ~~(V)$
where n=1, 2, 3… And that’s it. We can see that the area function does not affect the location of resonances. Finally, remember that, in average, the male oral tract has a length of 16.9 cm, and the female tract has an average length of 14.1 cm.

